![]() pour Re < 107
pour Re < 107
![]() pour Re > 107.
pour Re > 107.
III - Application au LASER
III-1) Caractéristiques du LASER:
Pour appliquer ces notions à un dériveur type LASER, il faut disposer des données nécessaires pour la coque et la voile.
Coque Laser:
Concernant la coque, un article de S. Gunther (site web Dr Laser) donne des caractéristiques " géométriques " obtenues par calculs (code Profile) pour un barreur de 70 kg:
- L = 3.84 m
- Smouillée = 2.98 m2
Une planche, tirée de l’article précité, donnant l’évolution de la force de friction et de la résistance d’onde en fonction de la vitesse, permet de déterminer les coefficients Cf et CW respectivement en fonction du nombre de Reynolds et du nombre de Froude. Il suffit de lisser quelques points par la " meilleure " fonction.
Les lissages retenus sont:
- pour Cf(Re), la formule de Prandtl Schliting
qui donne
|
|
-pour ![]() , donc une loi
exponentielle.
, donc une loi
exponentielle.
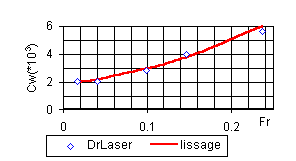
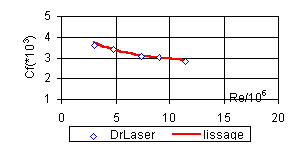
Figure 1
NB: La loi CW(Fr) est à prendre avec précaution: elle n’est valable que par mer plate et quand le bateau ne plane pas. Au delà d’une certaine vitesse, donc d’un nombre de Froude, le Laser plane, le coefficient CW s’écroule alors. Ce qui n’est pas pris en compte dans la loi CW(Fr) retenue.
Voile Laser:
Seule la surface de la voile est connue avec une relative précision: - Svoile = 7.1 m2. La polaire, à ma connaissance, n’a pas fait l’objet de recherches spécifiques. Pour cette application, la polaire retenue est donnée sur la figure ci-dessous. Les ordres de grandeur des coefficients sont corrects. La courbe a l’allure générale d’une voile de rapport d’aspect 2. C’est tout ce qu’on peut dire!
Le surcroît de puissance au voisinage de 20° est peut être exagéré. De même pour des incidences inférieures à 10°, le coefficient est certainement trop élevé. Ce n’est pas forcément génant pour les résultats les plus intéressants, dans la mesure où nous cherchons un réglage qui donne la vitesse maximale. g est alors à proximité de 20° quant c’est possible.
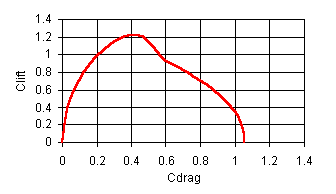
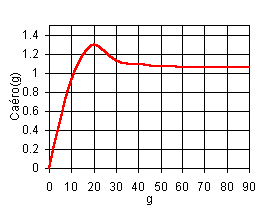
Figure 2
III-2) Vitesse d’un Laser pour un vent donné:
III-21) Le vent réel " souffle " à 10 m/s (36 km/h ou 19.4 noeuds - Force 5), quelle vitesse vais-je atteindre pour un cap de 40°, 90° et 150° par rapport au vent réel?
La résolution des équations précédentes avec g, orientation de la voile par rapport au vent apparent, permet de répondre à cette question.
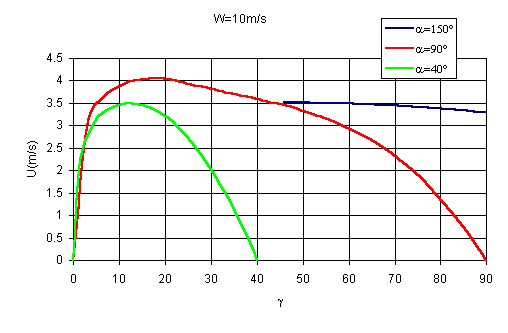
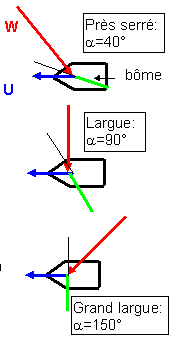
Figure 3
Avec un vent de 10 m/s, soit 19.4 noeuds, la vitesse calculée pour le Laser au près et au largue est de 3.5 m/s à 4 m/s soit 6.8 à 7.7 noeuds. Ces valeurs semblent un peu fortes. Un coefficient aérodynamique un peu élevé en est certainement la cause, d’où la nécessité de données plus précises pour la voile.
Commentaires:
Navigation en finesse: a £ 90°:
· un angle g = 0 correspond à la voile complètement choquée, face au vent, la force aérodynamique est nulle.
· un angle g = b correspond à la voile complètement bordée. La force aérodynamique n’est pas nulle mais est orientée perpendiculairement à l’axe du bateau. Il n’y donc pas de composante propulsive.
Ce qui explique pourquoi la vitesse est nulle pour les valeurs extrêmes de g: g = 0 et g = b.
· La valeur maximum de la vitesse est atteinte pour une valeur de g voisine de celle correspondant au maximum de Clift sur la polaire de la voile: g = 20°. La vitesse est très sensible à g. Un bon réglage est important.
Navigation en poussée: a > 90°:
· un angle g = b-90° correspond à la voile choquée, la bôme ne pouvant faire un angle supérieur à 90° avec l’axe du bateau
· un angle g > 90° est théoriquement possible, en bordant au delà du raisonnable. Un tel cas n’apparaît pas sur la courbe relative à a=150°. La valeur maximale considérée comme raisonnable ici est g = 90°. (Qui aurait l’idée d’amener la bôme dans l’axe du bateau aux allures portantes ?)
· la vitesse dépend faiblement de g ; elle est donc peu sensible au réglage.
III-22) Force propulsive et force antidérive en fonction de g pour une incidence a = 40° ?
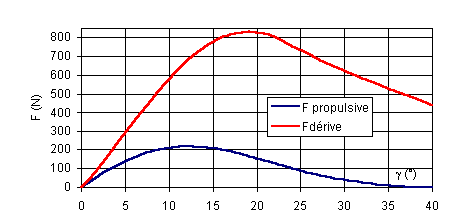
Figure 4
La force propulsive est maximale pour g
» 12°. En ce point la force de dérive est de 700 N. En retenant
pour le laser une distance de 2.5 m entre le centre de dérive (au milieu de la dérive) et
le centre de poussée (1/3 de la hauteur du mat), le couple de renversement à équilibrer par
le barreur est de 700x2.5 N.m = 1750 N.m. Il faut un barreur grand et lourd pour équilibrer
un tel couple: d » 1.1 à 1.2 m pour une taille raisonnable =>
le barreur doit peser 150 kg (![]() ) !.
) !.
Un barreur plus léger devra réduire le creux pour diminuer la force aérodynamique - étarquer la voile, et/ou naviguer avec une incidence g plus faible. Sur la figure 4, on constate que pour g = 7° la force de dérive ne vaut plus que 400 N; un barreur de 85 kg " suffit " alors. La force propulsive, et donc la vitesse sont faiblement réduite, est faiblement réduite: 10 % environ pour la force propulsive, 5% pour la vitesse.
Evidemment ces conclusions sont purement théoriques dans la mesure où la polaire de la voile LASER prise dans cet exemple ne représente certainement que faiblement la réalité. Les principes restent cependant valables. Chacun sait que par fort vent il vaut mieux " piquer " un maximum.
III-23) Vitesse du bateau en fonction de la vitesse du vent pour une incidence de 45° avec la direction du vent:
Sont représentées sur la figure 5, en fonction de la vitesse du vent:
· la vitesse du bateau U
· la résistance d’onde RW
· la résistance due au frottement de l’eau sur la coque: Rf
Pour des vents faibles, la force de frottement, ou friction, est prépondérante. Par contre dès que le vent forcit, c’est la résistance d’onde qui devient rapidement prépondérante. Dès un vent de 8m/s (15 noeuds) la vitesse du bateau évolue lentement en fonction du vent: U progresse de seulement 0.5 m/s quand W passe de 8 à 10 m/s. La vitesse du bateau tend vers une valeur limite.
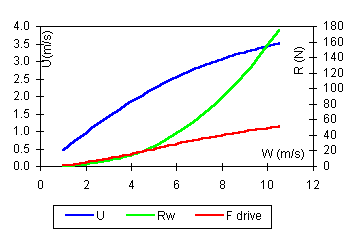
Figure 5
III-3) Polaire vitesse:
Les courbes de la figure 4 montrent qu’il existe une vitesse maximale correspondant au réglage optimal de la voile. En représentant chacun de ces points en fonction de l’angle a, nous obtenons la polaire vitesse du Laser.
Sur la courbe ci-dessous, l’angle a est orienté par rapport à la direction du vent avec la convention habituelle de la navigation: un angle de 20° correspond à une direction du bateau de 20° Est, un angle de 340° correspond à 20° (360°-20°) Ouest.
La vitesse dans la direction a par rapport au vent est égale à la longueur du segment OM. La composante dans l’axe du vent est Uy, et celle dans la direction perpendiculaire au vent est Ux.
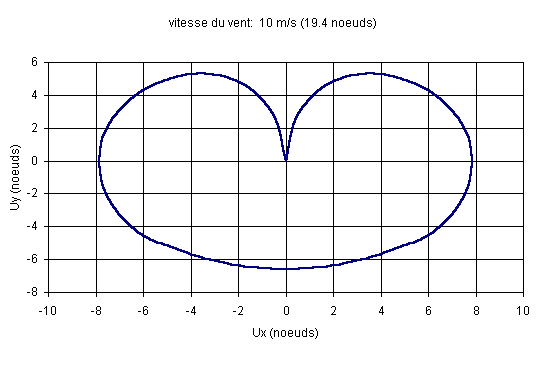
Figure 6
III-4) Utilisation des polaires vitesse pour la navigation:
1) Navigation au près en l’absence de courant:
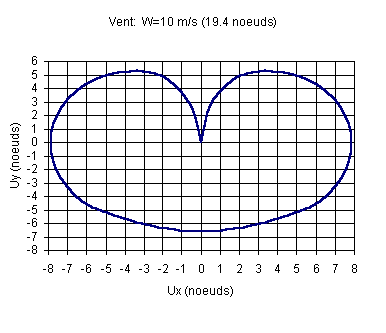 |
La composante utile de la vitesse est celle orientée dans la direction du vent. Pour que la durée de la remontée au vent soit minimale cette vitesse doit être maximale. L’allure de la courbe montre immédiatement que le cap idéal à suivre sur chacune des amures est ± 30° soit 30°E ou 30°W par rapport au vent. La vitesse du bateau est alors de 6.3 noeuds. La composante " utile " de la vitesse, c.a.d. suivant l’axe du vent, est de 5.3 noeuds. La vitesse du vent apparent est de 25 noeuds, et la déviation par rapport au vent réel de 7°. |
2) Navigation en présence d’un courant:
Considérons un courant animé d’une vitesse![]() sur
le plan d’eau. Son intensité est V et son orientation par rapport au vent réel est
y.
sur
le plan d’eau. Son intensité est V et son orientation par rapport au vent réel est
y.
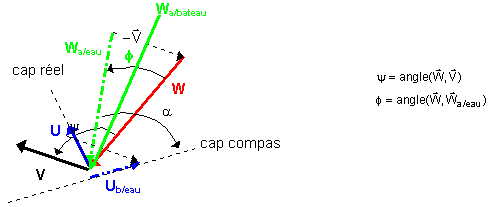
La vitesse apparente du vent par rapport au plan d’eau
est ![]() .
.
![]()
![]()
La vitesse du bateau par rapport à l’eau est égale à:
![]() . La direction de ce vecteur correspond
au cap compas suivi par la barreur.
. La direction de ce vecteur correspond
au cap compas suivi par la barreur.
La force hydrodynamique dépend de ![]() .
.
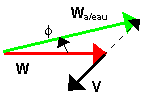
La force aérodynamique dépend de la vitesse apparente du vent par rapport au bateau:
![]()
La vitesse apparente du vent par rapport au bateau peut aussi s’écrire:
![]() .
.
En résumé les vitesses utiles sont ![]() et
et
![]() , respectivement utiles pour la force
hydrodynamique et la force aérodynamique.
, respectivement utiles pour la force
hydrodynamique et la force aérodynamique.
Sur un plan formel, le " problème " à résoudre est le même qu’en l’absence de
courant, à condition de remplacer ![]() par
par
![]() et
et
![]() par
par
![]() . L’angle
a correspond à l’angle entre
. L’angle
a correspond à l’angle entre
![]() et
et
![]() , et l’angle b
correspond à l’angle entre
, et l’angle b
correspond à l’angle entre![]() et
et
![]() .
.
La polaire vitesse par rapport à l’eau, s’obtient donc comme précédemment. Ensuite
la polaire vitesse par rapport au référentiel terrestre s’obtient en translatant la
polaire par rapport du vecteur courant ![]() et en lui faisant subir une rotation d’un angle
et en lui faisant subir une rotation d’un angle
![]() .
.
Considérons 2 exemples qui montrent l’intérêt de la polaire vitesse:
a) Un Laser navigue dans les conditions suivantes:
- vent 9m/s orienté W à 270°
- courant de 2 m/s orienté S/SE à 205°
L’angle entre le vent réel et le courant est donc de 65°
La vitesse du vent par rapport à l’eau est égale à:
![]() = 10 m/s
= 10 m/s
L’angle de déviation F est égal à 10.5°:
La polaire vitesse par rapport au vent apparent est donc celle déterminée au chapitre précédent.
Avec une translation de vecteur directeur
![]() et une rotation d’angle
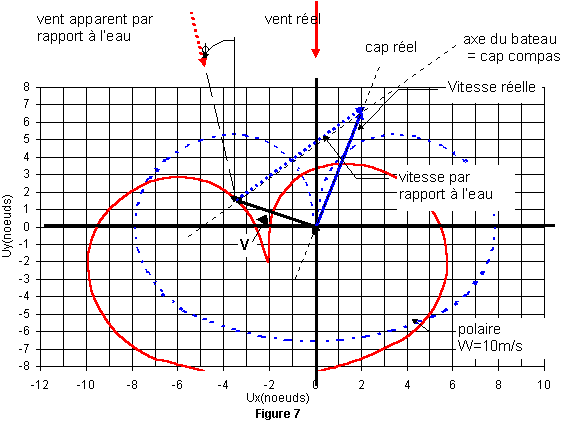
f, nous obtenons la polaire par rapport au vent réel (figure 7).
et une rotation d’angle
f, nous obtenons la polaire par rapport au vent réel (figure 7).
Cette polaire est utile pour choisir le cap compas du bateau de façon à arriver au plus vite à une bouée ou dans un port.
Par exemple, pour remonter dans l’axe du vent réel, la polaire montre qu’il suffit de suivre un cap compas de 30° par rapport au vent réel, c.a.d. 270 + 30° = 300°, soit 60° W. La vitesse réelle est alors de 7.5 noeuds.
b) Un Laser navigue dans les conditions suivantes:
- vent 11 m/s, ou 21 noeuds, orienté à 220° (S-SO)
- courant de 1.5 m/s, ou 2.9 noeuds, orienté à 85° (E)
L’angle entre le vent réel et le courant est donc de 135°. La vitesse du vent par rapport à
l’eau est égale à: ![]() = 10 m/s. L’angle
de déviation F est égal à 6.1°. Comme précédemment, la polaire par
rapport au vent réel, s’obtient à partir de celle de la figure 5 par une translationecteur
directeur
= 10 m/s. L’angle
de déviation F est égal à 6.1°. Comme précédemment, la polaire par
rapport au vent réel, s’obtient à partir de celle de la figure 5 par une translationecteur
directeur ![]() et une rotation d’angle
f : voir figure 8.
et une rotation d’angle
f : voir figure 8.
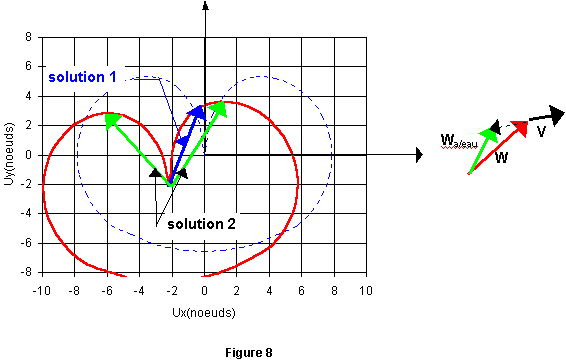
Pour remonter au mieux au vent, il y a 2 options intéressantes:
| - 1) en un seul bord babord amure (flèche bleue): | ||||
|
cap réel = axe du vent =220° cap compas/vent: 21° => cap compas 241 ° U = UY = 3.46 noeuds |
||||
| - 2) en 2 bords avec sur chacun des bords la composante UY maximale: | ||||
|
||||
Pour un trajet parfaitement dans l’axe du vent (bord de près d’un triangle olympique),
la durée de chacun des bords doit être telle que la distance parcourue dans la direction
perpendiculaire au vent soit la même sur les 2 bords: Donc:
![]()
=> ![]() .
.
La vitesse moyenne dans la direction du vent est alors:
![]() ,
,
soit ![]() = 3.71 noeuds
= 3.71 noeuds
Cette 2ème solution est donc la meilleure: elle se traduit par un gain de près de 10% sur la composante de la vitesse suivant la direction du vent, donc aussi de près de 10% sur la durée correspondante au trajet. Mais avec au moins un virement de bord en plus.